Latest

Google Search Engine

सोमवार, 9 सितंबर 2019

दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) - वज्र गुणनखण्ड विधि "Cross Multiplication"

दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) - वज्र गुणनखण्ड विधि "Cross Multiplication"

by on in

प्रश्नावली - 3.5

प्रश्न 1-
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/
(i)x - 3y - 3 = 0; 3x - 9y - 2 = 0
(ii) 2x + y = 5; 3x + 2y = 8
(iii) 3x - 5y = 20; 6x - 10y = 40
(iv)x - 3y - 7 = 0;3x - 3y - 15= 0

cross multiplication what is cross multiplication cross multiplication worksheet matrix multiplication cross multiplication method crossmultiplication whatiscrossmultiplication crossmultiplicationworksheet matrixmultiplication crossmultiplicationmethod #crossmultiplication #whatiscrossmultiplication #crossmultiplicationworksheet #matrixmultiplication #crossmultiplicationmethod,निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/ (i) x - 3y - 3 = 0; 3x - 9y - 2 = 0 (ii) 2x + y = 5; 3x + 2y = 8 (iii) 3x - 5y = 20; 6x - 10y = 40 (iv) x - 3y - 7 = 0; 3x - 3y - 15 = 0, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) by Ranjeet Sir, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables), दो चरों वाले रैखिक समीकरण, Linear Equations in Two Variables, दो चरों वाले रैखिक समीकरण, #दोचरोंवालेरैखिकसमीकरण, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3 #प्रतिस्थापनविधि, #रैखिकसमीकरणकाहल, #substitutionmethod, #दोचररैखिकसमीकरणकोहलकरना, #Class-10thNCERTगणित3.4, rkmsb.blogspot.com, www.rkmsb.blogspot.com #प्रतिस्थापनविधिmeaninginenglish, #कक्षा-10वीप्रतिस्थापनविधि, #rkmschannel, #ranjeetkumar, #mathmatics, #math, #docharowale rekhiksamikaran, rkmsb.blogspot.com, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3, प्रतिस्थापनविधि, रैखिकसमीकरणकाहल, substitutionmethod, दोचररैखिकसमीकरणकोहलकरना, Class-10thNCERTगणित3.3, प्रतिस्थापनविधिmeaninginenglish, कक्षा-10वीप्रतिस्थापनविधि, rkmschannel, ranjeetkumar, mathmatics, math, docharowale rekhiksamikaran, दो चरो वाले रैखिक समीकरण कक्षा 10 दो चरो वाले रैखिक समीकरण एवं असमिकाएं, दो चर वाले रैखिक समीकरण कक्षा 10 pdf, दो चर वाले रैखिक समीकरण कक्षा 10 ncert, दो चरो वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म 10th, दो चर वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म क्लास 10th, समीकरण को हल करना, प्रतिस्थापन विधि , सरल विधि, pratisthapan vidhi, pratisthapan vidi, saral vidi, saral vidhi, x y ke maan gyat karna , very imp question math, गणित के महत्वपूर्ण प्रश्न, वज्र गुणन विधि सूत्र, वज्र गुणन विधि formula, वज्र गुणन विधि समझाइए, वज्र गुणन विधि के सवाल, ब्रज गुणन विधि, वज्रगुणन विधि in English, वज्र गुणन विधि, वज्र गुणन विधि का सूत्र, वज्र गुणनखंड विधि का सूत्र, वज्र गुणन विधि से सवाल, वज्र गुणनखंड विधि समझाइए, वज्र गुणन विधि कक्षा 10, वज्र गुणनखंड, वज्र गुणनखंड विधि से सवाल, vajra gunan vidhi, वज्र गुणन विधि सूत्र, vilopan vidhi ke sawal bataye, vajra gunan vidhi in English, vajra gunan vidhi in hindi, vajra gunan vidhi formula, vajra gunan vidhi ka sutra, vajra gunan vidhi ka formula, cross multiplication, cross multiplication method, cross multiplication method formula, cross multiplication method in hindi, cross multiplication formula, cross multiply method, cross multiplication method worksheet, cross multiply formula, cross multiplication class 10, cross multiplication of vectors, cross multiplication of linear equations, cross multiplication of fractions, cross multiplication of matrices, cross multiplication of 3 equations, cross multiplication of equations, cross multiplication of three vectors, cross multiplication of 2 equation, cross multiplication of quadratic equation, cross multiplication of two quadratic equations, cross multiplication method
Cross Multiplication 

उत्तर 1- 
इस प्रश्न को हल करने से पहले ये जान लेते है कि हम कैसे जानेंगे कि रैखिक समीकरण के युग्म एक अद्वितीय हल है या कोई हल नहीं है या अपरिमित रूप से अनेक हल हैं/
यदि समीकरण a1x + b1y + c1 = 0 और समीकरण a2x + b2y + c2 = 0 हो/
तो, 
cross multiplication what is cross multiplication cross multiplication worksheet matrix multiplication cross multiplication method crossmultiplication whatiscrossmultiplication crossmultiplicationworksheet matrixmultiplication crossmultiplicationmethod #crossmultiplication #whatiscrossmultiplication #crossmultiplicationworksheet #matrixmultiplication #crossmultiplicationmethod,निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/ (i) x - 3y - 3 = 0; 3x - 9y - 2 = 0 (ii) 2x + y = 5; 3x + 2y = 8 (iii) 3x - 5y = 20; 6x - 10y = 40 (iv) x - 3y - 7 = 0; 3x - 3y - 15 = 0, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) by Ranjeet Sir, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables), दो चरों वाले रैखिक समीकरण, Linear Equations in Two Variables, दो चरों वाले रैखिक समीकरण, #दोचरोंवालेरैखिकसमीकरण, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3 #प्रतिस्थापनविधि, #रैखिकसमीकरणकाहल, #substitutionmethod, #दोचररैखिकसमीकरणकोहलकरना, #Class-10thNCERTगणित3.4, rkmsb.blogspot.com, www.rkmsb.blogspot.com #प्रतिस्थापनविधिmeaninginenglish, #कक्षा-10वीप्रतिस्थापनविधि, #rkmschannel, #ranjeetkumar, #mathmatics, #math, #docharowale rekhiksamikaran, rkmsb.blogspot.com, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3, प्रतिस्थापनविधि, रैखिकसमीकरणकाहल, substitutionmethod, दोचररैखिकसमीकरणकोहलकरना, Class-10thNCERTगणित3.3, प्रतिस्थापनविधिmeaninginenglish, कक्षा-10वीप्रतिस्थापनविधि, rkmschannel, ranjeetkumar, mathmatics, math, docharowale rekhiksamikaran, दो चरो वाले रैखिक समीकरण कक्षा 10 दो चरो वाले रैखिक समीकरण एवं असमिकाएं, दो चर वाले रैखिक समीकरण कक्षा 10 pdf, दो चर वाले रैखिक समीकरण कक्षा 10 ncert, दो चरो वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म 10th, दो चर वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म क्लास 10th, समीकरण को हल करना, प्रतिस्थापन विधि , सरल विधि, pratisthapan vidhi, pratisthapan vidi, saral vidi, saral vidhi, x y ke maan gyat karna , very imp question math, गणित के महत्वपूर्ण प्रश्न, वज्र गुणन विधि सूत्र, वज्र गुणन विधि formula, वज्र गुणन विधि समझाइए, वज्र गुणन विधि के सवाल, ब्रज गुणन विधि, वज्रगुणन विधि in English, वज्र गुणन विधि, वज्र गुणन विधि का सूत्र, वज्र गुणनखंड विधि का सूत्र, वज्र गुणन विधि से सवाल, वज्र गुणनखंड विधि समझाइए, वज्र गुणन विधि कक्षा 10, वज्र गुणनखंड, वज्र गुणनखंड विधि से सवाल, vajra gunan vidhi, वज्र गुणन विधि सूत्र, vilopan vidhi ke sawal bataye, vajra gunan vidhi in English, vajra gunan vidhi in hindi, vajra gunan vidhi formula, vajra gunan vidhi ka sutra, vajra gunan vidhi ka formula, cross multiplication, cross multiplication method, cross multiplication method formula, cross multiplication method in hindi, cross multiplication formula, cross multiply method, cross multiplication method worksheet, cross multiply formula, cross multiplication class 10, cross multiplication of vectors, cross multiplication of linear equations, cross multiplication of fractions, cross multiplication of matrices, cross multiplication of 3 equations, cross multiplication of equations, cross multiplication of three vectors, cross multiplication of 2 equation, cross multiplication of quadratic equation, cross multiplication of two quadratic equations, cross multiplication method
Cross Multiplication 

 (i) x - 3y - 3 = 0   .....(1)
    3x - 9y - 2 = 0  .....(2)
समीकरण (1) की a1x + b1y + c1 = 0 से तुलना करने पर,
a1= 1, b1 = -3, c1 = -3

 तथा समीकरण (2) की a2x + b2y + c2 = 0 से तुलना करने पर,
a2= 3, b2 = -9, c2 = -2
cross multiplication what is cross multiplication cross multiplication worksheet matrix multiplication cross multiplication method crossmultiplication whatiscrossmultiplication crossmultiplicationworksheet matrixmultiplication crossmultiplicationmethod #crossmultiplication #whatiscrossmultiplication #crossmultiplicationworksheet #matrixmultiplication #crossmultiplicationmethod,निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/ (i) x - 3y - 3 = 0; 3x - 9y - 2 = 0 (ii) 2x + y = 5; 3x + 2y = 8 (iii) 3x - 5y = 20; 6x - 10y = 40 (iv) x - 3y - 7 = 0; 3x - 3y - 15 = 0, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) by Ranjeet Sir, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables), दो चरों वाले रैखिक समीकरण, Linear Equations in Two Variables, दो चरों वाले रैखिक समीकरण, #दोचरोंवालेरैखिकसमीकरण, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3 #प्रतिस्थापनविधि, #रैखिकसमीकरणकाहल, #substitutionmethod, #दोचररैखिकसमीकरणकोहलकरना, #Class-10thNCERTगणित3.4, rkmsb.blogspot.com, www.rkmsb.blogspot.com #प्रतिस्थापनविधिmeaninginenglish, #कक्षा-10वीप्रतिस्थापनविधि, #rkmschannel, #ranjeetkumar, #mathmatics, #math, #docharowale rekhiksamikaran, rkmsb.blogspot.com, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3, प्रतिस्थापनविधि, रैखिकसमीकरणकाहल, substitutionmethod, दोचररैखिकसमीकरणकोहलकरना, Class-10thNCERTगणित3.3, प्रतिस्थापनविधिmeaninginenglish, कक्षा-10वीप्रतिस्थापनविधि, rkmschannel, ranjeetkumar, mathmatics, math, docharowale rekhiksamikaran, दो चरो वाले रैखिक समीकरण कक्षा 10 दो चरो वाले रैखिक समीकरण एवं असमिकाएं, दो चर वाले रैखिक समीकरण कक्षा 10 pdf, दो चर वाले रैखिक समीकरण कक्षा 10 ncert, दो चरो वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म 10th, दो चर वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म क्लास 10th, समीकरण को हल करना, प्रतिस्थापन विधि , सरल विधि, pratisthapan vidhi, pratisthapan vidi, saral vidi, saral vidhi, x y ke maan gyat karna , very imp question math, गणित के महत्वपूर्ण प्रश्न, वज्र गुणन विधि सूत्र, वज्र गुणन विधि formula, वज्र गुणन विधि समझाइए, वज्र गुणन विधि के सवाल, ब्रज गुणन विधि, वज्रगुणन विधि in English, वज्र गुणन विधि, वज्र गुणन विधि का सूत्र, वज्र गुणनखंड विधि का सूत्र, वज्र गुणन विधि से सवाल, वज्र गुणनखंड विधि समझाइए, वज्र गुणन विधि कक्षा 10, वज्र गुणनखंड, वज्र गुणनखंड विधि से सवाल, vajra gunan vidhi, वज्र गुणन विधि सूत्र, vilopan vidhi ke sawal bataye, vajra gunan vidhi in English, vajra gunan vidhi in hindi, vajra gunan vidhi formula, vajra gunan vidhi ka sutra, vajra gunan vidhi ka formula, cross multiplication, cross multiplication method, cross multiplication method formula, cross multiplication method in hindi, cross multiplication formula, cross multiply method, cross multiplication method worksheet, cross multiply formula, cross multiplication class 10, cross multiplication of vectors, cross multiplication of linear equations, cross multiplication of fractions, cross multiplication of matrices, cross multiplication of 3 equations, cross multiplication of equations, cross multiplication of three vectors, cross multiplication of 2 equation, cross multiplication of quadratic equation, cross multiplication of two quadratic equations, cross multiplication method
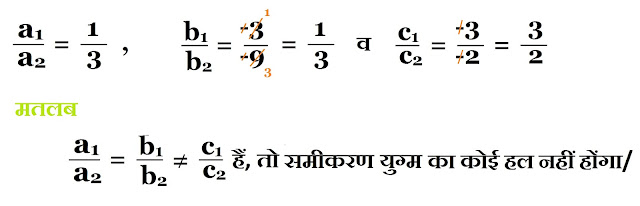Cross Multiplication 

 (ii) 2x + y = 5   
            या 
2x + y - 5 = 0   .....(1)

        3x + 2y = 8
              या
3x + 2y - 8 = 0  .....(2)

 समीकरण (1) की a1x + b1y + c1 = 0 से तुलना करने पर,
a1= 2, b1 = 1, c1 = -5

तथा समीकरण (2) की a2x + b2y + c2 = 0 से तुलना करने पर,

a2= 3, b2 = 2, c2 = -8
cross multiplication what is cross multiplication cross multiplication worksheet matrix multiplication cross multiplication method crossmultiplication whatiscrossmultiplication crossmultiplicationworksheet matrixmultiplication crossmultiplicationmethod #crossmultiplication #whatiscrossmultiplication #crossmultiplicationworksheet #matrixmultiplication #crossmultiplicationmethod,निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/ (i) x - 3y - 3 = 0; 3x - 9y - 2 = 0 (ii) 2x + y = 5; 3x + 2y = 8 (iii) 3x - 5y = 20; 6x - 10y = 40 (iv) x - 3y - 7 = 0; 3x - 3y - 15 = 0, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) by Ranjeet Sir, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables), दो चरों वाले रैखिक समीकरण, Linear Equations in Two Variables, दो चरों वाले रैखिक समीकरण, #दोचरोंवालेरैखिकसमीकरण, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3 #प्रतिस्थापनविधि, #रैखिकसमीकरणकाहल, #substitutionmethod, #दोचररैखिकसमीकरणकोहलकरना, #Class-10thNCERTगणित3.4, rkmsb.blogspot.com, www.rkmsb.blogspot.com #प्रतिस्थापनविधिmeaninginenglish, #कक्षा-10वीप्रतिस्थापनविधि, #rkmschannel, #ranjeetkumar, #mathmatics, #math, #docharowale rekhiksamikaran, rkmsb.blogspot.com, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3, प्रतिस्थापनविधि, रैखिकसमीकरणकाहल, substitutionmethod, दोचररैखिकसमीकरणकोहलकरना, Class-10thNCERTगणित3.3, प्रतिस्थापनविधिmeaninginenglish, कक्षा-10वीप्रतिस्थापनविधि, rkmschannel, ranjeetkumar, mathmatics, math, docharowale rekhiksamikaran, दो चरो वाले रैखिक समीकरण कक्षा 10 दो चरो वाले रैखिक समीकरण एवं असमिकाएं, दो चर वाले रैखिक समीकरण कक्षा 10 pdf, दो चर वाले रैखिक समीकरण कक्षा 10 ncert, दो चरो वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म 10th, दो चर वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म क्लास 10th, समीकरण को हल करना, प्रतिस्थापन विधि , सरल विधि, pratisthapan vidhi, pratisthapan vidi, saral vidi, saral vidhi, x y ke maan gyat karna , very imp question math, गणित के महत्वपूर्ण प्रश्न, वज्र गुणन विधि सूत्र, वज्र गुणन विधि formula, वज्र गुणन विधि समझाइए, वज्र गुणन विधि के सवाल, ब्रज गुणन विधि, वज्रगुणन विधि in English, वज्र गुणन विधि, वज्र गुणन विधि का सूत्र, वज्र गुणनखंड विधि का सूत्र, वज्र गुणन विधि से सवाल, वज्र गुणनखंड विधि समझाइए, वज्र गुणन विधि कक्षा 10, वज्र गुणनखंड, वज्र गुणनखंड विधि से सवाल, vajra gunan vidhi, वज्र गुणन विधि सूत्र, vilopan vidhi ke sawal bataye, vajra gunan vidhi in English, vajra gunan vidhi in hindi, vajra gunan vidhi formula, vajra gunan vidhi ka sutra, vajra gunan vidhi ka formula, cross multiplication, cross multiplication method, cross multiplication method formula, cross multiplication method in hindi, cross multiplication formula, cross multiply method, cross multiplication method worksheet, cross multiply formula, cross multiplication class 10, cross multiplication of vectors, cross multiplication of linear equations, cross multiplication of fractions, cross multiplication of matrices, cross multiplication of 3 equations, cross multiplication of equations, cross multiplication of three vectors, cross multiplication of 2 equation, cross multiplication of quadratic equation, cross multiplication of two quadratic equations, cross multiplication method
Cross Multiplication 
(iii) 3x - 5y = 20
               या 
        3x - 5y - 20 = 0   .....(1)

   6x - 10y = 40
           या 
 6x - 10y - 40 = 0   .....(2)
समीकरण (1) की a1x + b1y + c1 = 0 से तुलना करने पर,
a1= 3, b1 = -5, c1 = -20

तथा समीकरण (2) की a2x + b2y + c2 = 0 से तुलना करने पर,


a2= 6, b2 = -10, c2 = -40
cross multiplication what is cross multiplication cross multiplication worksheet matrix multiplication cross multiplication method crossmultiplication whatiscrossmultiplication crossmultiplicationworksheet matrixmultiplication crossmultiplicationmethod #crossmultiplication #whatiscrossmultiplication #crossmultiplicationworksheet #matrixmultiplication #crossmultiplicationmethod,निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/ (i) x - 3y - 3 = 0; 3x - 9y - 2 = 0 (ii) 2x + y = 5; 3x + 2y = 8 (iii) 3x - 5y = 20; 6x - 10y = 40 (iv) x - 3y - 7 = 0; 3x - 3y - 15 = 0, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) by Ranjeet Sir, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables), दो चरों वाले रैखिक समीकरण, Linear Equations in Two Variables, दो चरों वाले रैखिक समीकरण, #दोचरोंवालेरैखिकसमीकरण, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3 #प्रतिस्थापनविधि, #रैखिकसमीकरणकाहल, #substitutionmethod, #दोचररैखिकसमीकरणकोहलकरना, #Class-10thNCERTगणित3.4, rkmsb.blogspot.com, www.rkmsb.blogspot.com #प्रतिस्थापनविधिmeaninginenglish, #कक्षा-10वीप्रतिस्थापनविधि, #rkmschannel, #ranjeetkumar, #mathmatics, #math, #docharowale rekhiksamikaran, rkmsb.blogspot.com, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3, प्रतिस्थापनविधि, रैखिकसमीकरणकाहल, substitutionmethod, दोचररैखिकसमीकरणकोहलकरना, Class-10thNCERTगणित3.3, प्रतिस्थापनविधिmeaninginenglish, कक्षा-10वीप्रतिस्थापनविधि, rkmschannel, ranjeetkumar, mathmatics, math, docharowale rekhiksamikaran, दो चरो वाले रैखिक समीकरण कक्षा 10 दो चरो वाले रैखिक समीकरण एवं असमिकाएं, दो चर वाले रैखिक समीकरण कक्षा 10 pdf, दो चर वाले रैखिक समीकरण कक्षा 10 ncert, दो चरो वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म 10th, दो चर वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म क्लास 10th, समीकरण को हल करना, प्रतिस्थापन विधि , सरल विधि, pratisthapan vidhi, pratisthapan vidi, saral vidi, saral vidhi, x y ke maan gyat karna , very imp question math, गणित के महत्वपूर्ण प्रश्न, वज्र गुणन विधि सूत्र, वज्र गुणन विधि formula, वज्र गुणन विधि समझाइए, वज्र गुणन विधि के सवाल, ब्रज गुणन विधि, वज्रगुणन विधि in English, वज्र गुणन विधि, वज्र गुणन विधि का सूत्र, वज्र गुणनखंड विधि का सूत्र, वज्र गुणन विधि से सवाल, वज्र गुणनखंड विधि समझाइए, वज्र गुणन विधि कक्षा 10, वज्र गुणनखंड, वज्र गुणनखंड विधि से सवाल, vajra gunan vidhi, वज्र गुणन विधि सूत्र, vilopan vidhi ke sawal bataye, vajra gunan vidhi in English, vajra gunan vidhi in hindi, vajra gunan vidhi formula, vajra gunan vidhi ka sutra, vajra gunan vidhi ka formula, cross multiplication, cross multiplication method, cross multiplication method formula, cross multiplication method in hindi, cross multiplication formula, cross multiply method, cross multiplication method worksheet, cross multiply formula, cross multiplication class 10, cross multiplication of vectors, cross multiplication of linear equations, cross multiplication of fractions, cross multiplication of matrices, cross multiplication of 3 equations, cross multiplication of equations, cross multiplication of three vectors, cross multiplication of 2 equation, cross multiplication of quadratic equation, cross multiplication of two quadratic equations, cross multiplication method
Cross Multiplication 

 (iv) x - 3y - 7 = 0   .....(1)
    3x - 3y - 15 = 0   .....(2)
समीकरण (1) की a1x + b1y + c1 = 0 से तुलना करने पर,
a1= 1, b1 = -3, c1 = -7

तथा समीकरण (2) की a2x + b2y + c2 = 0 से तुलना करने पर,



a2= 3, b2 = -3, c2 = -15
cross multiplication what is cross multiplication cross multiplication worksheet matrix multiplication cross multiplication method crossmultiplication whatiscrossmultiplication crossmultiplicationworksheet matrixmultiplication crossmultiplicationmethod #crossmultiplication #whatiscrossmultiplication #crossmultiplicationworksheet #matrixmultiplication #crossmultiplicationmethod,दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) - वज्र गुणनखण्ड विधि , निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं/ अद्वितीय हल की स्थिति में, उसे वज्र-गुणन विधि से ज्ञात कीजिए/ (i) x - 3y - 3 = 0; 3x - 9y - 2 = 0 (ii) 2x + y = 5; 3x + 2y = 8 (iii) 3x - 5y = 20; 6x - 10y = 40 (iv) x - 3y - 7 = 0; 3x - 3y - 15 = 0, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables) by Ranjeet Sir, दो चरों वाले रैखिक समीकरण(Linear Equations in Two Variables), दो चरों वाले रैखिक समीकरण, Linear Equations in Two Variables, दो चरों वाले रैखिक समीकरण, #दोचरोंवालेरैखिकसमीकरण, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3 #प्रतिस्थापनविधि, #रैखिकसमीकरणकाहल, #substitutionmethod, #दोचररैखिकसमीकरणकोहलकरना, #Class-10thNCERTगणित3.4, rkmsb.blogspot.com, www.rkmsb.blogspot.com #प्रतिस्थापनविधिmeaninginenglish, #कक्षा-10वीप्रतिस्थापनविधि, #rkmschannel, #ranjeetkumar, #mathmatics, #math, #docharowale rekhiksamikaran, rkmsb.blogspot.com, #rkmschannel, #NCERT10, #कक्षादसवीं-प्रतिस्थापनविधि()-प्रश्नावली3.3, प्रतिस्थापनविधि, रैखिकसमीकरणकाहल, substitutionmethod, दोचररैखिकसमीकरणकोहलकरना, Class-10thNCERTगणित3.3, प्रतिस्थापनविधिmeaninginenglish, कक्षा-10वीप्रतिस्थापनविधि, rkmschannel, ranjeetkumar, mathmatics, math, docharowale rekhiksamikaran, दो चरो वाले रैखिक समीकरण कक्षा 10 दो चरो वाले रैखिक समीकरण एवं असमिकाएं, दो चर वाले रैखिक समीकरण कक्षा 10 pdf, दो चर वाले रैखिक समीकरण कक्षा 10 ncert, दो चरो वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म 10th, दो चर वाले रैखिक समीकरण कक्षा 9, दो चर वाले रैखिक समीकरण युग्म क्लास 10th, समीकरण को हल करना, प्रतिस्थापन विधि , सरल विधि, pratisthapan vidhi, pratisthapan vidi, saral vidi, saral vidhi, x y ke maan gyat karna , very imp question math, गणित के महत्वपूर्ण प्रश्न, वज्र गुणन विधि सूत्र, वज्र गुणन विधि formula, वज्र गुणन विधि समझाइए, वज्र गुणन विधि के सवाल, ब्रज गुणन विधि, वज्रगुणन विधि in English, वज्र गुणन विधि, वज्र गुणन विधि का सूत्र, वज्र गुणनखंड विधि का सूत्र, वज्र गुणन विधि से सवाल, वज्र गुणनखंड विधि समझाइए, वज्र गुणन विधि कक्षा 10, वज्र गुणनखंड, वज्र गुणनखंड विधि से सवाल, vajra gunan vidhi, वज्र गुणन विधि सूत्र, vilopan vidhi ke sawal bataye, vajra gunan vidhi in English, vajra gunan vidhi in hindi, vajra gunan vidhi formula, vajra gunan vidhi ka sutra, vajra gunan vidhi ka formula, cross multiplication, cross multiplication method, cross multiplication method formula, cross multiplication method in hindi, cross multiplication formula, cross multiply method, cross multiplication method worksheet, cross multiply formula, cross multiplication class 10, cross multiplication of vectors, cross multiplication of linear equations, cross multiplication of fractions, cross multiplication of matrices, cross multiplication of 3 equations, cross multiplication of equations, cross multiplication of three vectors, cross multiplication of 2 equation, cross multiplication of quadratic equation, cross multiplication of two quadratic equations, cross multiplication method
Cross Multiplication 
एक कदम प्रगति की ओर .......................
By at
Labels:

कोई टिप्पणी नहीं:

एक टिप्पणी भेजें

आपने हमारी पोस्ट के लिए अपना कीमती समय निकाला उसके लिए बहुत बहुत धन्यवाद/ हम आपकी राय जानने के लिए उत्सुक हैं/ कृपया एक प्यारा सा कमेन्ट करने का कष्ट करें/

सदस्यता लें टिप्पणियाँ भेजें (Atom)